高级光照

Share

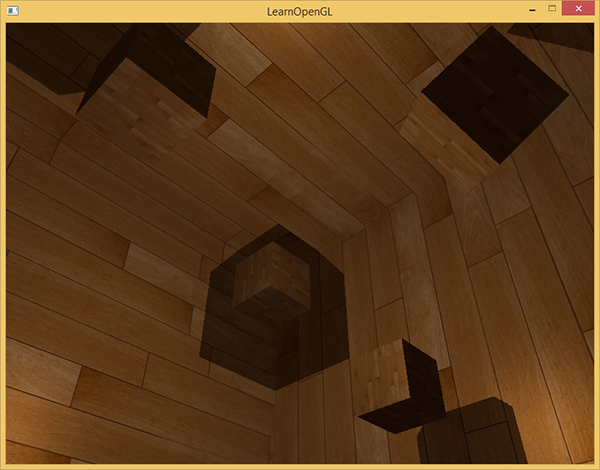
1 Blinn-Phong光照

使用半程向量与法向量之间的角度代替视线与反射向量之间的角度，其它与Phong光照一致。

优点：

  • 计算快
  • 当角度超过90度时不会出现异常的光照(Phong会产生异常的光照，因为cos超过90度为负数)

2 Gamma校正

人眼感知的非线性：相当于物理亮度的2次幂

显示器的非线性：相当于物理亮度的2.2次幂(CRT显示器)

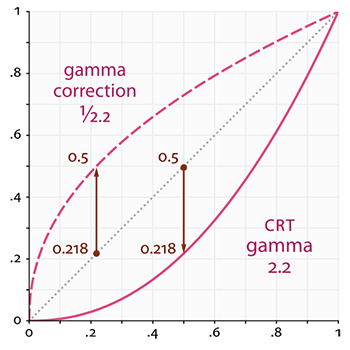
但是显示器的衰减+人眼的衰减，就使得人眼看起来的亮度不太正常，同时由于很多光照的计算都是在线性空间内进行的，所以需要进行Gamma校正，使显示器显示的颜色是线性的。

在OpenGL中，通常有两种方法来完成Gamma校正：

  • 使用OpenGL内建的sRGB帧缓冲

    1
    glEnable(GL_FRAMEBUFFER_SRGB);

  • 自己在片元着色器中手动Gamma校正

    1
    fragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));

3 sRGB纹理

如果我们在屏幕上取图片，那么这个图片是线性的(经过Gamma校正)，如果我们拿这个图片再进行一次渲染，那么这个图片再经过一次Gamma校正，会变得不正常，OpenGL提供了一种解决方案，即GL_SRGB和GL_SRGB_ALPHA内部纹理格式，这些图片不会再进行一次Gamma校正。

1
glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);

4 衰减

真实的物理世界中光照的衰减和距离的平方成反比，因此下列公式在Gamma校正后使用是没有问题的，可以产生可信的效果：

但是如果没有Gamma校正，那么线性函数更适合用于光照衰减的计算。(见左下和右上)

因为显示器的非线性替代了光照衰减的非线性，使得两者效果相似。

5 阴影映射(Shadow Mapping)

以光的位置为视角进行渲染，看得到的被点亮，看不到的就在阴影之中。

主要实现方法是利用帧缓冲的深度缓冲，以光源的位置为视角渲染深度贴图。然后在正式渲染的时候使用深度贴图，将片元位置映射到光空间中，对同样的x和y，对比z和深度贴图的值，如果z值大于深度贴图，那么说明此片元在阴影中，shadow值置为1，否则在阴影外，shadow值置为0，shadow值与blinn-phong的漫反射、镜面反射交互作用，得到最终片元的值。

阴影贴图的改进

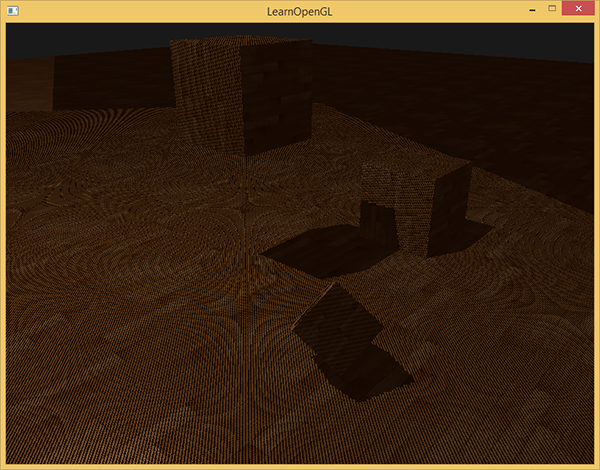
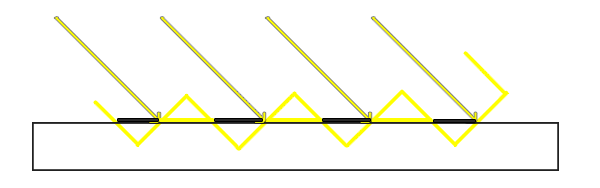
如果出现阴影失真(Shadow Acne)，如上图所示，在地板上和正方体上出现了很短的阴影条，一般是因为多个片元从同一个深度值进行采样，因此可以使用阴影偏移(Shadow Bias)解决这个问题，即在比较z值和深度值时加入一个偏移:

1
2
float bias = 0.005;
float shadow = currentDepth - bias > closestDepth  ? 1.0 : 0.0;

有些坡度大的仍然会产生阴影失真，一个更可靠的方法是根据表面朝向光线的角度更改偏移量:

1
float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);

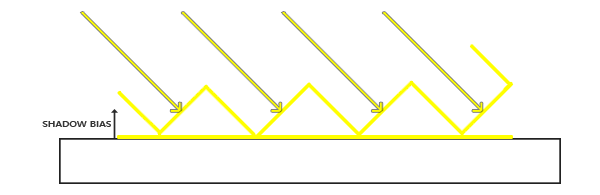
效果:

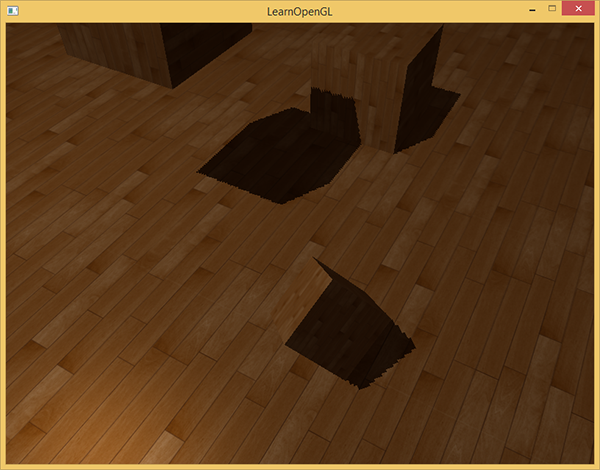
悬浮

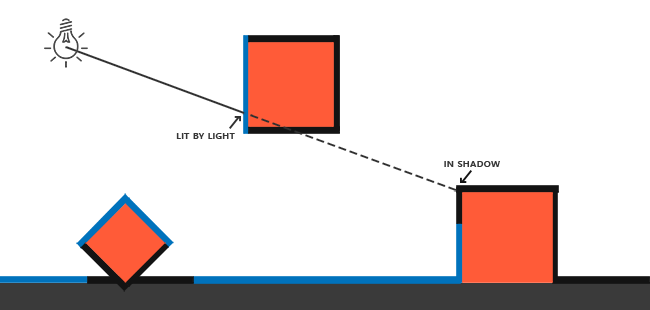
使用阴影偏移的一个缺点是你对物体的实际深度应用了平移。偏移有可能足够大，以至于可以看出阴影相对实际物体位置的偏移，你可以从下图看到这个现象（这是一个夸张的偏移值）：

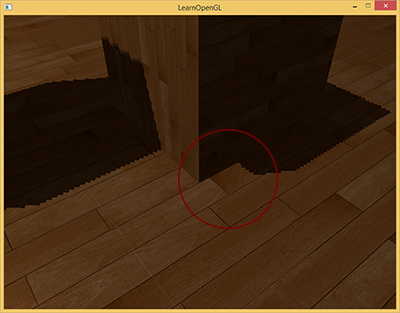
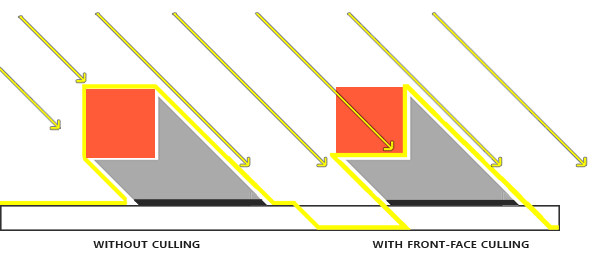
这叫悬浮(Peter Panning)，解决这个问题的一个方法是使用正面剔除，即只使用背面的z值来对深度值进行比较，正面剔除对于不同的场景需要进行更详细的考虑。

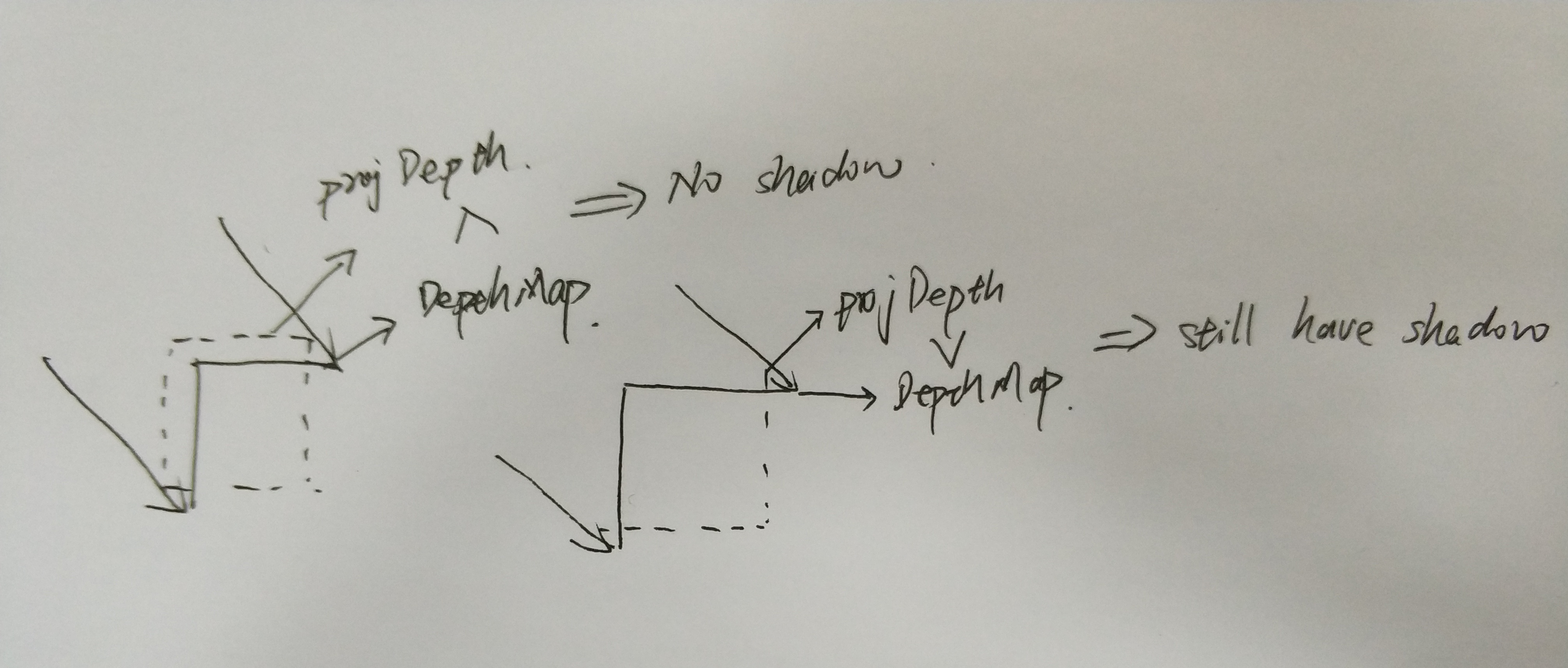
6 万向阴影贴图

由于上一节的阴影贴图是具有方向性的，只能对一个区域的物体渲染阴影，得到一个窗口的阴影贴图，因此考虑全局的阴影，需要使用深度立方体贴图，想象一个点光源对所有方向放出光，一个窗口显然是不够用的，考虑一个包围点光源的立方体，光源对所有方向的深度贴图都可以对应到正方体内部的一个面，这样我们只需要6个面就可以完成全局的阴影贴图。

与单方向的阴影贴图不同的是，这里需要使用几何着色器，指定将图形渲染到立方体的哪一个面，另外，不需要再将片元坐标转换到光空间窗口进行深度值比对，只需要确定片元坐标到光源的方向向量，求出向量的长度即片元的深度，再获取这个方向上深度贴图的closestDepth值，这个值由于是0到1的值，需要再乘以一个far_plane的值才能得到可与实际深度对比的深度值，将片元深度与closestDepth进行对比，得到shadow值，在阴影中为1，否则为0。再对blinn-phong的参数作用，确认片元的最终颜色。

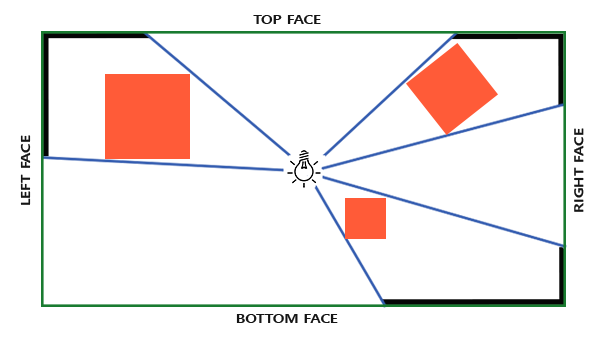
最终效果如下：